Hãy lập trình nhập vào số nguyên ~n~, thực hiện thay thế các chữ số ~0~ trong biểu diễn thập phân của ~n~ thành các chữ số ~5~ và in ra kêt quả. Ví dụ: Với ~n=1005~ thì sau khi thực hiện thay thế ta thu được số ~1555~. Còn với ~n=1234~, thì không có chữ số nào bị thay thế và kết quả vẫn là số ~1234~.

Input

Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa một số nguyên ~n~.

Output

Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra số ~n~ sau khi thay thế các chữ số của ~n~ theo yêu cầu đề bài.

Constraints

• ~1 \leq T \leq 10^5 ; 0 \leq n \leq 10^{12}~.

Sample Input

2
1000
1234

Sample Output

1555
1234

Bạn được tặng một con xúc xắc hình khối lập phương với ~6~ mặt. Mỗi mặt của con xúc xắc có in một số chấm, số lượng chấm trong phạm vi từ ~1~ đến ~6~, giống như bất kỳ con xúc xắc thông thường nào. Bạn được biết số chấm trên một mặt của xúc xắc, nhiệm vụ của bạn là đoán số ở mặt đối diện của xúc xắc.

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa một số nguyên ~n~ cho biết số chấm trên một mặt của con xúc xắc.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra số ~n~ sau khi thay thế các chữ số của ~n~ theo yêu cầu đề bài.

Ràng buộc:

• ~1 \leq T \leq 500 ; 1 \leq n \leq 6~.

Ví dụ:

Input

2
6
2

Output

1
5

Có ~N~ bệnh nhân đến khám tại phòng khám. Giả sử rằng cứ sau ~X~ (phút) thì có một bệnh nhân mới đến phòng khám. Ngoài ra, bác sĩ sẽ chỉ dành ~10~ phút để khám cho mỗi bệnh nhân. Nhiệm vụ của bạn là tính toán thời gian (bằng phút) mà bệnh nhân cuối cùng cần phải chờ đến lượt mình được bác sĩ khám bệnh.

Input

Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa hai số nguyên ~N~ và ~X~.

Output

Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số ~M~ là số phút mà bệnh nhân cuối cùng cần chờ bác sĩ tại phòng khám.

Constraints

• ~1 \le T \le 500; 1 \le N \le 100; 0 \le X \le 30~.

Sample Input

5
4 5
5 3
6 5
7 6
8 2

Sample Input

15
28
25
24
56

Cho số nguyên không dấu ~N~. Hãy kiểm tra tính chẵn lẻ của ~N~. Trong bài toán này tính chẵn lẻ của ~N~ là số bit ~1~ trong biểu diễn nhị phân của ~N~. Nghĩa là nếu trong biểu diễn nhị phân của ~N~ có chứa một số chẵn các bit ~1~ thì ~N~ được coi là có tính chẵn, và ngược lại thì ~N~ có tính lẻ. Ví dụ: ~N=13_{10}=1101_2~ nên ~N~ có tính lẻ, còn ~N=9_{10}=1001_2~ nên có tính chẵn.

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa số nguyên ~N~.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa thông báo "odd" nếu ~N~ có tính lẻ và "even" nếu ~N~ có tính chẵn.

Ràng buộc

• ~1 \leq T \leq 500 ; 0 \leq N \leq 10^{12}~.

Ví dụ:

Input

2
13
9

Input

odd
even

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa số nguyên ~N~.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số lượng tin nhắn cần gửi để ~N~ học sinh đều nhận được tất cả ~N~ câu chuyện hài.

Ràng buộc:

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^5~.

Ví dụ:

Input

1 
2

Output

2

Một số được gọi là "số tam giác" nếu ta có thể biểu diễn nó dưới dạng lưới hình tam giác gồm các điểm sao cho các điểm tạo thành một tam giác đều, tức là hàng đầu tiên có một điểm, hàng thứ hai có hai điểm, hàng thứ ba có ba điểm.... Các số tam giác bắt đầu là ~1,3(=1+2), 6(=1+2+3)~, ~10(=1+2+3+4)~, xem hình minh họa sau:

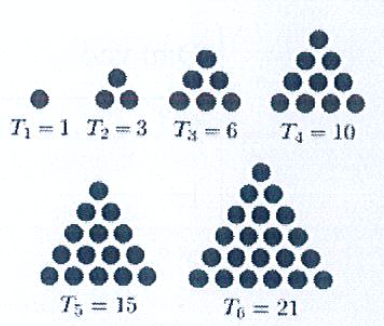
Yêu cầu: Cho biết số nguyên dương ~N~, hãy cho biết ~N~ có phải số tam giác hay không?

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa số nguyên ~N~ duy nhất.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số ~1~ nếu ~N~ là số tam giác, ngược lại thì in ra số ~0~ .

Ràng buộc:

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^7~.

Ví dụ:

Input

5
3
4
6
55
345

Output

1
0
1
1
0

Có ~N~ con chuột ở trong một đường hầm thẳng hẹp, chỉ cho phép ~1~ con chuột ở một chỗ tại một thời điểm, có ~N~ cái tổ chuột nằm dọc theo đường hầm, mỗi cái tổ chỉ chứa vừa một con chuột. Một con chuột có thể ở nguyên vị trí của nó, hoặc di chuyển một bước sang phải từ vị trí ~x~ sang ~x+1~ hoặc di chuyển một bước sang trái từ ~x~ đến ~x-1~. Một bước di chuyển tiêu tốn ~1~ phút. Giả sử đường hầm là trục số nguyên ~Ox~, biết vị trí ~N~ con chuột và ~N~ tổ chuột, hãy tính số phút tối thiểu để con chuột cuối cùng chui được vào tổ.

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ là số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm:
  • Dòng đầu chứa số nguyên ~N~.
  • Dòng thứ ~2~ chứa ~N~ số nguyên khác nhau cho biết vị trí của ~N~ con chuột.
  • Dòng thứ ~3~ chứa ~N~ số nguyên khác nhau cho biết vị trí của ~N~ tổ chuột.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số phút tối thiểu để con chuột cuối cùng chui được vào tổ.

Ràng buộc

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^4~.
• Vị trí của các con chuột và tổ chuột là số nguyên có giá trị tuyệt đối không quá ~10^7~.

Sample Input

1
3
4 -4 2
4 0 5

Sample Input

4

Mèo Tom và chuột Jerry đang chơi một trò chơi để phân định, ai thắng sẽ được lấy miếng phô mai cuối cùng trong tủ lạnh. Trò chơi như sau: Cho một số nguyên dương ~N~, hai người chơi luân phiên. Tom chơi trước, ai tới lần chơi, sẽ phải tìm một số nguyên ~a(a \lt N)~ là ước của ~N~, sau đó ~N~ sẽ bị trừ đi ~a~. Ai không tìm được số ~a~ nữa sẽ là người thua cuộc. Cho biết số ~N~, bạn hãy xác định Tom hay Jerry thắng.

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa số nguyên ~N~.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số ~1~ nếu Tom thắng hoặc số ~0~ nếu Jerry thắng.

Ràng buộc

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^6~.

Ví dụ:

Sample Input

2
2
4

Sample Input

1
1

Cho số nguyên ~N~. Hãy thực hiện lặp lại một số lần thao tác sau cho đến khi thu được số ~N~ có ~1~ chữ số. Cụ thể thao tác là: Thay ~N~ bằng tổng các chữ số của ~N~.

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa số nguyên ~N~.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng chứa số ~N~ cuối cùng.

Ràng buộc:

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^9~.

Ví dụ:

Sample Input

2
1
98

Sample Input

1
8

Cho số nguyên ~N~, và một số nguyên tố ~p~ tìm lũy thừa lớn nhất của ~p~ mà là ước của ~N~ ! ( ~N~ ! tức là ~N~ giai thừa).

Dữ liệu:

• Dòng đầu tiên của đầu vào chứa số nguyên ~T~ cho biết số bộ dữ liệu cần kiểm tra. Mỗi bộ dữ liệu gồm một dòng chứa hai số nguyên ~N~ và ~p~.

Kết quả:

• Ứng với mỗi bộ dữ liệu đầu vào, chương trình của bạn cần in ra một dòng số mũ lớn nhất của lũy thừa cơ số ~p~ mà là ước của ~N!~.

Ràng buộc:

• ~1 \leq T \leq 100 ; 1 \leq N \leq 10^5 ; 2 \leq p \leq 10^5~.

Ví dụ:

Sample Input

3
62 7
76 2
3 5

Sample Input

9
73
0